《探索三角形相似的条件》

教学设计

温县武德镇徐堡初级中学  成前进

学习目标：

知识目标：

1、掌握两角判定两个三角形相似的条件；

2、会利用相似三角形判定方法来计算或证明

情感态度价值观

1、通过动手操作，小组合作探索两个相似三角形的条件的过程，进一步领悟类比的思想方法；

2、在探索过程之后，能有条理地、清晰地阐述自己的观点

教学重点：掌握相似三角形判定定理，及其应用

教学难点：领悟类比的思想及有条理地、清晰地阐述自己的观点

教学方法与教学手段：

利用几个简单问题，引发学生思考、回答，调动起学生学习本节内容的积极性，在此基础上，引发学生大胆猜想，并整理出相关框架，导入本节课题。

利用上面的三个猜想，发动同桌二人进行合作学习，指导完成猜想，并归纳总结相似三角形的判定方法一。

利用判定一引导学生分类思维：各个特殊三角形的相似特点，做到应用结论，解决问题，培养学生思考问题、解决问题的能力；进一步将图形进行变形，小组讨论、展示交流，得出常见三角形的相似特点，这样可以培养学生灵活运用知识的能力，增强学生的创新意识和创新能力。

通过课堂练习，当堂检测学生的学习情况，进行查漏补缺，突出重难点内容；鼓励学生将本节内容进行总结，提高学生的归纳能力和口头表达能力。

复习引新：

教师：利用多媒体的几何画板出示：

1、你能用自己的话说一下什么是相似多边形？

2、相似的符号如何书写？记两个多边形相似时，要注意什么？

3、最简单的多边形时什么图形？

4、类比相似多边形，什么是相似三角形？

学生回答

通过学生回答，即使学生清楚地明白上节课学习的内容，起到一个复习的作用，也是学生清晰知道了本节课的内容，相似三角形，利用类比的思想进行类比。得出结论：

两个三角形，三边对应成比例，各角都相等的三角形相似。动手合作，类比探究

议一议：

两个三角形相似至少满足几个条件，你有那些经验？

学生：全等三角形时，需要三个条件

这三个条件都有哪些？

学生：SSS、SAS、ASA、AAS直角三角形的HL；

那两个三角形相似,我们该从哪些方面考虑呢？

学生：边、角

那我们就从角开始进行探索吧！

想一想：

有一个角对应相等两个三角形相似吗？

学生：不相似，如△ABC和△ANM、△ABC和△AED就有一个角相等，但这两个三角形就不相似

那两个角对应相等的两个

三角形相似吗？

学生：有的说相似，有的说不相似

同伴合作：

同桌两人，左边画△ABC，右边画△A'B'C',使得

∠A=∠A'=45°，∠B=∠B'=60°

此时：此时：∠C=∠C'吗？                      自己有什么方法解决，然后在小组进行讨论，最后小组派代表进行交流；    

从而引出课题《探索相似三角形的条件》

 学生经过一番自己的画法、探索利用三角板的刻度进行测量，然后在小组内进行交流后，以及教师利用几何画板进行演示，最终得出：两个角对应相等的两个三角形相似。

牛刀小试：

1、有一个锐角相等的两个直角三角形相似吗？

2、顶角相等的两个等腰三角形相似吗？

3、有一个角是30°的两个等腰三角形相似吗？

4、有一个角是120°的两个等腰三角形相似吗？

5、在△ABC和△DEF中，∠A=∠D=70°,∠B=60°,∠E=50°,这两个三角形相似吗？

通过牛刀小试，使学生真正了解“两个角相等的两个三角形相似”的计算；

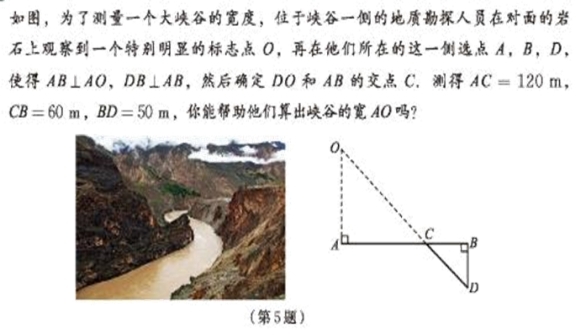应用计算：

通过应用计算，使学生明白数学来源于生活，又为生活解决问题。

拓展延伸：

如图，在△ABC中，∠BAC=90°,AD⊥BC,垂足为D.指出图中所有的相似三角形；并说明为什么？

△BAD∼△ACD（∠BDA=∠ADC=90°,∠1=∠C）

△BAD∼△BCA（∠BDA=∠BAC=90°,∠B=∠C）

△BAC∼△ADC（∠BAC=∠ADC=90°,∠B=∠2）

通过拓展延伸，使学生了解只要两个三角形由两个角对应相等，就能得出这两个三角形相似。

小结：

1、今天你有什么收获？从知识和方法上来说

2、你还有哪些困惑？

通过学生说的收获和困惑，既复习了本节课的知识点，又为下节课及以后奠定了一部分基础。