4.3 一次函数的图象

第1课时 正比例函数的图象和性质

一 、教学目标

1.了解一次函数的图象是一条直线， 能熟练作出一次函数的图象.

2.经历函数图象的作图过程，初步了解作函数图象的一般步骤：列表、描点、连线.

3.已知函数的代数表达式作函数的图象，培养学生数形结合的意识和能力.

4.理解一次函数的代数表达式与图象之间的一一对应关系.

二、教学重难点

初步了解作函数图象的一般步骤：列表、描点、连线.

教学难点

理解一次函数的代数表达式与图象之间的一一对应关系.

三、教学方法

目标导学法、合作探究法

四、教学过程

第一环节：复习回顾

1.在下列函数中,（1)y=x²-3  （2)y=2x （3）y= 1/x（4）y=2-5x是一次函数的是             ，是正比例函数的是      

2.函数有哪些表示方法?

第二环节：画正比例函数的图象

一、师生互动，探究新知

出示例1:画出正比例函数y=2x的图象教师引导学生一起作图，并得出画函数图象的方法及步骤.

描点法画函数图象的步骤:列表、描点、连线.

【设计意图】通过学生的猜想、验证等探究活动，使学生亲自经历知识的生成过程,让学生体验到成功的快乐，并且激发了他们探究的欲望，在潜移默化中让学生体验“数”与“形”的转化过程,感受函数图象的直观性，激发学生学习数学的兴趣.问题:满足关系式y=2x的x，y所对应的点(x，y)是否都在它的图象上?正比例函数y=2x的图象上的点都满足它的关系式吗?

活动一:首先让同学们说出几对满足关系式y=2x的x，y的值;

活动二:教师利用PPT在平面直角坐标系中找到x、y对应的点(x，y)的位置，并验证这些点是否在函数y=2x的图象上.在正比例函数y=2x的图象上找出一些点，并验证这些点的坐标(x，y)是否满足关系式.

活动三:通过验证师生共同总结:

点在函数图象上（形）与点的坐标满足函数关系式(数)

【设计意图】通过PPT上的图像将抽象的内容清晰、形象、生动地展示在学生面前，便于学生理解函数关系式与图象的对应关系，从而达到突出重点，突破难点的目的，起到了事半功倍的教学效果.

练习:画出下列函数的图象:

(1)y=-2x

各小组拿出课前准备好的坐标纸,进行小组合作学习,学生们通过互帮互助，交流学习,准确画出函数图象，然后让学生在黑板上进行展示.最后引导学生深层次地归纳出正比例函数图象的特点:

1.正比例函数y=kx的图象是经过点(0，0)的一条直线.

2.画正比例函数图象的简便方法:“两点法".

二、活动探究,总结性质

做一做:用简便方法在同一平面直角坐标系内作出下列正比例函数的图象.

(1)y=x (2)y=是½x（3）y=3x（4）y=-x(5)y=-½x(6)y=-3x

各小组拿出课前准备好的坐标纸，进行小组合作学习，学生们通过互帮互助,交流学习，准确画出函数图象.

【设计意图】让学生熟练掌握画图的技能,同时为后续总结正比例函数图象的性质提供素材.

议一议:观察正比例函数的图象，它们经过哪几个象限，这是由什么值决定的?

【设计意图】让学生通过对函数图象的观察与比较，归纳出正比例函数中k对函数分布性和增减性的影响.通过几何画板将抽象的内容清晰、形象、生动地展示在学生面前.同时，培养学生数形结合的观察、思考问题的意识和能力.

观察图象，总结得出正比例函数图象及性质:正比例函数y=kx(k≠0)当k>0时，图象经过第一、三象限，y随x的增大而增大;当k<0时，图象经过第二、四象限，y随x的增大而减小；k的绝对值越大，直线越接近y轴.

第三环节：讲解例题

例2 已知正比例函数y=(m+1)xm²  ，它的图象经过第几象限？

变式1：  已知正比例函数y=(k+1)x

（1）若函数图象经过第一、三象限，则k的取值范围是________

（2）若函数图象经过点（2，4），则k_=____

（3）变式2：当x＞0时，y与x的函数解析式为y=2x ，当x≤0时，y与x的函数解析为y=-2x ，则在同一直角坐标系中的图象大致为(  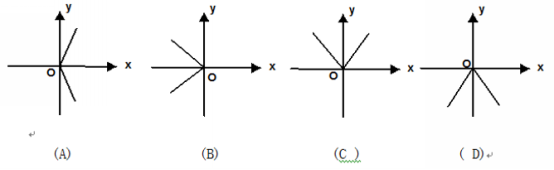  ) 2

例3 已知正比例函数y=mx的图象经过点（m，4），且y的值随着x值的增大而减小，求m的值

练习1 已知正比例函数y=kx (k>0)的图象上有两点（x1，y1），（x2，y2），若x1<x2，则y1       y2

练习2 正比例函数y=k1x和y=k2x的图象如图，则k1和k2的大小关系是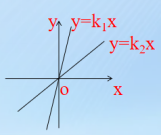（    ）l2

第四环节：巩固练习，深化理解

  1. 下列图象哪个可能是函数y=-x的图象（      ）0

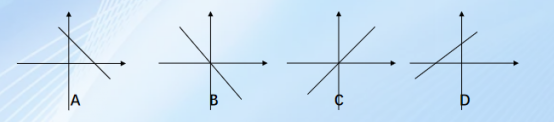
2.对于正比例函数y =（k-2）x，当x 增大时，y 随x 的增大而增大，则k的取值范围 (  )

3.函数y=-7x的图象经过第_________象限，经过点_______与点 _______ ，y随x的增大而_______.

4.已知正比例函数y=(2m+4)x.

（1）当m             ，函数图象经过第一、三象限；

（2）当m             ，y 随x 的增大而减小；

（3）当m              ，函数图象经过点（2，10）

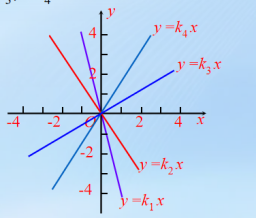55. 如图分别是函数y=k1 x，y=k2 x，y=k3 x，y=k4x的图象.

（1）k1       k2，k3       k4(填“>”或“<”或“=”)；

（2）用不等号将k1， k2， k3， k4及0依次连接起来.

目的：这里的5个练习题，一是让学生熟练正比例函数图象的作法，二是明确正比例函数图象的性质，要注意自变量的取值范围.

效果：学生通过练习，进一步熟练了正比例函数图象的作法，对正比例函数和正比例函数图象的一般特征有了清楚的认识.

第五环节：课时小结

内容：本节课我们通过对正比例函数图象的研究，掌握了以下内容：

（1）函数与图象之间是一一对应的关系.

（2）画函数的图象的一般步骤.

（3）正比例函数的图象和性质.

目的：让学生在回忆的过程中，进一步加深对正比例函数图象的理解，同时对本节所学知识有一个总结性的认识.

效果：学生通过对本节学习的回顾和小结，对所学知识更清楚，抓住了重点，明确了关键.

第六环节：作业布置

习题4.3   第2、4题必做，第5题选做

第七环节：板书设计

4.3一次函数的图象

（第一课时）

正比例函数图象是一条经过原点的直线，画正比例函数图象时我们只需描点(0，0)和点 (1，k)，连线即可.

正比例函数图象的性质：

k＞0时图象经过第一、三象限，y的值随着x值的增大而增大；k＜0时图象经过第二、四象限，y的值随着x值的增大而减小；|k|越大，直线越接近y轴.