第四章 三角形

1认识三角形

（第1课时）三角形的概念及内角和

一 学生分析

学生的知识技能基础：学生在小学已经学习了有关三角形的一些初步知识，能在生活中抽象出三角形的几何图形，并能给出三角形的简单概念及一些相关概念.但不够严密，教师要在教学中指出，并要相对严密地给出概念.学生在第二章对两直线平行的条件以及平行线的特征进行了探索，使学生具备了利用平行线的结论得出三角形内角和的结论的基本知识和基本技能．

学生的活动经验基础：学生在以前的几何学习过程中,已对图形的概念、线段及角的表示法、线段的测量等有了一定的认识,为认识三角形概念、表示法的学习奠定了基础.在小学学习三角形的内角和的结论时是通过撕、拼的方法得到的，具备了直观操作的经验，同时在以前的数学学习中学生已经经历了很多合作学习的过程，具有了一定的合作学习的经验，具备了一定的合作与交流的能力．

二 教学任务分析

让学生掌握三角形的概念，能指出三角形的顶点、边、角等特点，能用适当的符号表示三角形以及这些特点；经历探索、验证“三角形内角和等于180°”的活动过程，获得一定的推理活动经验；能应用三角形内角和定理解决一些简单的问题；能运用直角三角形两锐角互余的性质解决简单的问题；会按角的大小关系对三角形分类，能判断出给定三角形的形状．基于此，本节课的教学目标是：

(1)知识与技能：掌握三角形的概念；通过观察、操作、想象、推理“三角形内角和等于180°”的活动过程,发展空间观念,有条理地表达能力．

(2)过程与方法：让学生在数学活动中通过相互间的合作与交流，培养学生的相互协作意识及数学表达能力．

(3)情感与态度：在探究学习中体会数学的现实意义，培养学习数学的信心，体验解决问题方法的多样性．

◆活动1　创设情境　导入新课（课件）活动内容 ：复习线和角的研究路径，引出三角形，类比线和角的研究路径，指出三角形的研究方向。

◆活动2　实践探究　交流新知

【探究1】认识三角形及边，角，顶点

1参照几组图片,提出有什么共同的特点？生活中的三角形,以及为什么设计成三角形?

【归纳】三角形具有稳定性。

2（课件）观察下面屋顶的结构：

问题：(1)你能从图①中找出几个不同的三角形吗？

(2)这些三角形有什么共同的特点？

【归纳】由不在同一直线上的三条线段首尾顺次相接所组成的图形叫作三角形．“三角形”可以用符号“△”表示，顶点是A，B，C的三角形，记作△ABC.△ABC的三边，有时也用a，b，c来表示．顶点A所对的边BC用a表示，边AC、边AB分别用b，c来表示．

【探究2】三角形的内角和

我们知道，将一个三角形的三个角撕下来，拼在一起，可以得到三角形三个内角的和为180°.小明只撕下三角形的一个角，也得到了上面的结论．你能说出其中的道理吗？

(1)如图①，剪一个三角形纸片，它的三个内角分别为∠1，∠2和∠3.

(2)将∠1撕下，按图②所示进行摆放，其中∠1的顶点与∠2的顶点重合，它的一条边与∠2的一条边重合．此时∠1的另一条边b与∠3的边a平行吗？　平行　，理由是　内错角相等，两直线平行　Ｗ．

(3)如图③，将∠3与∠2的公共边延长，它与b所夹的角为∠4，∠3与∠4的大小有什么关系？　相等　，理由是　两直线平行，同位角相等　Ｗ．

【归纳】用平行线的性质与判定以及平角的性质证明三角形三个内角的和等于180°.

【探究3】三角形的分类

●置疑导入　（多媒体出示）

（三兄弟之争）在一个直角为老大的三角形村庄里，住着三个内角，平时他们非常团结，有一天，老三不高兴了，对老大说“凭什么你的度数最大，我也要和你一样大！”老大说：“这是不可能的，否则我们这个家就要被拆散，围不起来了！”“为什么呢？”老二、老三纳闷起来……

同学们，你们知道其中的道理吗？

【教学与建议】教学：置疑三角形的最大角问题，培养学生的学习兴趣，激发学生的求知欲．建议：引导学生对问题思考、讨论、探究．

议一议：下面我们共同做一个猜角的游戏，观察图①中小明所拿三角形被遮住的两个内角是什么角？小颖的呢？试着说明理由．图②中小亮所拿三角形被遮住的两个内角可能是什么角？

解：图①中小明所拿三角形是钝角三角形，被遮住的两个内角都是锐角；小颖所拿的是直角三角形，被遮住的两个内角也都是锐角．图②三角形无法确定．

【归纳】我们可以按三角形内角的大小把三角形分为三类：

　　【探究4】直角三角形两个锐角之间的数量关系

填表：Rt△ABC中，∠C＝90°.

　　【归纳】直角三角形的两个锐角互余．

◆活动3　开放训练　应用举例

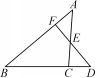
【例1】如图，D是△ABC中BC边延长线上一点，F为AB上一点，FD交AC于点E，∠DFB＝90°，∠A＝46°，∠D＝50°.求∠ACB的度数．

【方法指导】在△DFB中，根据三角形内角和定理，求得∠B的度数，再在△ABC中求∠ACB的度数即可．

解：在△DFB中，因为∠DFB＝90°，∠D＝50°，

所以∠B＝180°－∠DFB－∠D＝180°－90°－50°＝40°.

在△ABC中，因为∠A＝46°，∠B＝40°，

所以∠ACB＝180°－∠A－∠B＝180°－46°－40°＝94°.

◆活动4　

【学生活动】你这节课的主要收获是什么？还有哪些疑惑？

【教学说明】梳理三角形相关概念和性质，加深理解．

◆活动5　

【当堂检测】：1观察下面的三角形，并把它们的标号填入相应的圈内．

【方法指导】根据三角形内角的大小，将三角形分类．

2，图中一共有多少个三角形？锐角三角形、直角三角形、钝角三角形各有多少个？用符号表示这些三角形．

【方法指导】根据三角形的定义和三角形的分类：三个角都是锐角的三角形是锐角三角形；有一个角是直角的三角形是直角三角形；有一个角是钝角的三角形是钝角三角形，即可解答问题．

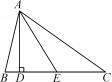
解：共有6个三角形．

其中锐角三角形有2个：△ABE，△ABC；

直角三角形有3个：△ABD，△ADE，△ADC；

钝角三角形有1个：△AEC.

【作业】课本P92～93习题4.1中的T1、T2、T3 .

本节课培养学生善于观察生活、乐于探索研究的学习品质，使他们能很好地找出生活中的三角形的实例．让学生在轻松愉快的氛围中自然地得到三角形的定义．

通过小组讨论、直观教具演示等手段，激发了学生学习的兴趣，了解特殊三角形的性质与其形状有关——直角三角形的两个锐角互余．通过对三角形分类的学习，使学生了解数学分类的基本思想．