课程基本信息

学科

数学

年级

七年级

学期

春季

课题

你有多少种画平行线的方法

教科书

书  名：义务教育教科书  七年级  下册

出版社：人民教育出版社               出版日期：2024年4月

教学目标

1.掌握不同画平行线的方法。

2.积极参与数学活动，在数学活动过程中，充分利用所学知识，发挥想象力。

3.在合作交流中，体验获得成功和学习数学的兴趣。

教学内容

教学重点：用平行线的判定方法画平行线。

教学难点：动手操作画出正确的图形。

教学过程

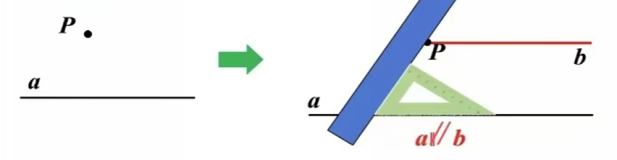
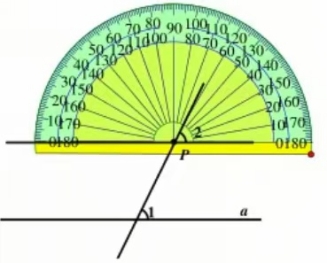
一、 探究新知

操作：关于平行线，我们已经学了判定和性质。现在我们来认识画平行线的方法。那么，过直线外一点如何画这条直线的平行线呢？

请同学们取出准备好的纸、笔，现在纸上画一条直线a，并取直线外一点P，过点P画直线a的平行线。

教师：如何说明画的直线与已知直线平行？（ “同位角相等，两直线平行”。）

探究1：李明的画法

教师：李明同学没有带三角尺，只有两量角器和直尺，能画出平行线吗？

教师边让几何画板演示，边讲解。

画法：

1.过点P任画一条直线与直线a相交；

2.用量角器量出∠1的度数，以点P为顶点画∠2=∠1；

3.反向延长∠2的边。

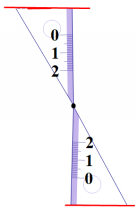
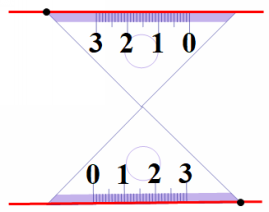
总结李明的画法：同位角相等，两直线平行。

教师：平行线的判定方法还有哪些？

学生：内错角相等，两直线平行。

同旁内角互补，两直线平行。

教师：是否可以通过画内错角相等或者同旁内角互来画平行线？

（让学生动手操作，教师巡视并演示）

拓展延伸：如果是两个含45°或30°角的直角三角形，你能摆出平行线吗？

  教师预设：

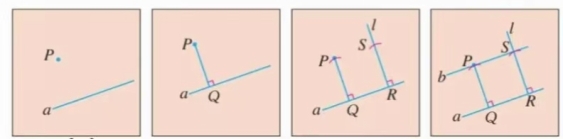
探究2：刘伟的画法

教师：刘伟同学也有不同画平行线的方法

画法：

1.画PQ⊥a；

2.画l⊥a，取RS=PQ；

3.连接PS，则b∥a。

追问1：刘伟同学是构造出了一个什么图形？（长方形）

拓展延伸：你还有其它的构图方法吗？

预设：构造平行四边形、构造等梯形、构造全等三角形

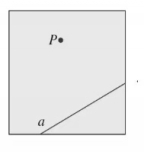
归纳总结：以上画法主要从两个角度入手：一种画法是从平行线的判定入手，利用同位角相等或内错角相等或同旁内角互补从而得到两直线平行；另一种是构造特殊的图形，利用对边平行来画的。

教师：以上都是通过三角板、量角器等工具来画平行线的，如果不利用工具，能否直接通过其它的方法比如折纸得出平行线呢？

探究3王芳的折纸法

如图，在一张半透明的正方形纸上任取一点P，然后画一条直线a，如何折出过点P与a？

师生活动：学生折一折，试一试，并说明理由，学生上台演示。

思考：如图是王芳同学通过折纸画的，根据王芳同学的操作过程，尝试这折一次试试，你能说出其中的数学道理吗？

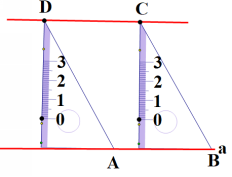
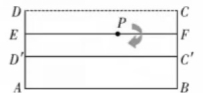
利用折纸的方法，两次折出的都是垂线，利用两个交点处的角都是直角，很容易通过角的关系来说明得到的是平行线。

拓展延伸：如果把正方形换成长方形，其余条件不变，你能否折出平行线呢？同学们加小组合作探究。（可以折出平行线，交点处都是直角）如果把已知条件换成平行四边形、梯形，其他条件不变，能否折出平行线呢？（能折出平行线）

问题：如图，在一张半透明的长方形纸ABCD内部任取一点P，请过点P折出长方形的一边AB所在直线的平行线，并说明理由。

师生活动：学生折一折，试一试，画出折痕。教师请学生上台演示折法并说明理由。

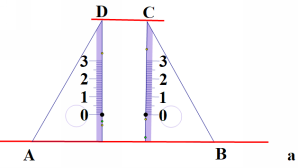
教师追问：这样折叠，对折法有什么要求吗？（折痕要经过点P且翻折后点D和点C都要在矩形短边上）

延伸、思考：教师演示折纸法，学生跟着一起操作。并让学生思考怎样证明这种折纸法折出的是平行线，即CD∥OE

折法：对折使角的一边OA与角的另一边OB重合，过点D折叠使点O与点C重合，连接CD，此时CD∥OB。

二、课堂小结

1.本节课你有哪些收获？

2.本节课你学会哪些画图技巧？

3.你还有什么疑惑？

教师：你还有其他方法吗？课下请与同学们交流一下。

布置作业：总结画平行线的方法。

板书设计：

活动1 你有说少种画平行线的方法

利用平行线的判定作图

   利用平行四边形的特征作图

利用平行线的判定折纸