中小学教师信息技术与课程融合课教学设计

（文本型）

课例名称：等腰三角形

学段、学科：初中  数学

教材版本：人教版

任课教师：周娇艳

联系电话：15993756321

一、教材及教学内容分析：

本节课选自人教版初中数学八年级上册第十三章第三节第一课时，属于“图形与几何”领域的内容。等腰三角形是三角形中的一种特殊形式，其性质定理“等边对等角”和“三线合一”是初中几何中的重要知识点，为后续学习等边三角形、相似三角形以及圆的相关知识奠定基础。本节课在教材中起着承上启下的作用，既是对前面三角形知识的深化，又是后面学习复杂几何图形的基础。

二、教学对象分析：

本节课的教学对象是八年级学生，他们已经掌握了三角形的基本概念和性质，具备了一定的几何推理能力。然而，对于等腰三角形这一特殊图形的性质，他们可能还停留在直观感知阶段，缺乏系统的理论证明。此外，八年级学生正处于逻辑思维发展的关键期，对抽象概念的接受能力逐渐增强，但仍需借助具体实例和动手操作来加深理解。因此，在教学中应注重引导学生通过探究、合作、交流等方式，主动构建知识体系。从年龄特点来看，八年级学生思维活跃、爱表现，抓住学生的这一特点，采用形象生动、形式多样的教学方法和学生广泛的、积极主动参与的学习方式，能激发学生兴趣，高效地完成教学目标。

根据以上学生的特点，在正式上课之前，通过国家中小学智慧教育平台班级群向学生发送预习作业，了解学生预习后对知识的掌握情况。

（1）判断题

1.等腰三角形的顶角一定是锐角.

2.等腰三角形的底角可能是锐角或者直角、钝角都可以.

3.钝角三角形不可能是等腰三角形.  

4.等腰三角形的顶角平分线一定垂直底边.

5.等腰三角形的角平分线、中线和高互相重合.

6.等腰三角形底边上的中线一定平分顶角.

（2）如图，在△ABC中，AB = AC，D是BC边上的中点，∠B = 30°，

求 ∠BAD 和 ∠ADC的度数.

通过调查发现，学生对等腰三角形的第一个性质：等边对等角的基础题掌握还好，课堂上可以进行这个性质的提高性训练；但对于第二个性质：三线合一掌握不好，分不清是哪三线合一，对于这个性质的应用需要加强练习。

3、教学目标

（一）核心素养目标（2022版新课标要求）

数学抽象：通过观察、操作抽象出等腰三角形的定义和性质。

逻辑推理：经历“猜想→验证→证明”的探究过程，发展演绎推理能力。

直观想象：借助几何画板动态演示，理解“等边对等角”“三线合一”的几何特征。

数学建模：运用等腰三角形性质解决实际测量问题

数学运算：计算等腰三角形的角度、边长及相关几何量。

（二）知识与技能目标

1.能准确表述等腰三角形的定义，识别生活中的等腰三角形。

2.掌握并证明“等边对等角”“三线合一”的性质定理。

3.能利用性质解决简单的几何计算与证明问题。

（三）过程与方法目标

1、通过折纸、测量、观察等活动，经历数学发现的完整过程。

2、学会用数学语言表达几何命题，体会转化思想与分类讨论思想。

四、教学重难点及解决措施：

教学重难点及解决措施：

1.理解并掌握等腰三角形的性质.(重点)

2.经历等腰三角形的性质的探究过程，能初步运用等腰三角形的性质解决有关问题.(难点)

解决措施：

1.通过学生动手操作、flsh动画演示、几何画板演示发现等腰三角形的两个性质，然后进行猜想，再通过小组讨论证明方法，师生交流得到相关定理。并提示学生几何用语如何使用。

2.最后通过典型例题分析和当堂练习，初步运用等腰三角形的性质解决有关问题

五、媒体工具与技术应用：

1.flsh动画演示

2.几何画板

3.鸿合多屏互动

4.PPT

教学过程：

教学环节一：导入新课

教师活动：

先展示一组生活中的等腰三角形图片，接着提出问题：

1. “这些图形有什么共同特点？它们为什么会被广泛应用于建筑和设计中？”

2.回顾三角形的定义，并认识等腰三角形的腰、底边、顶角、底角的相关概念。

2.回顾三角形的定义，并认识等腰三角形的腰、底边、顶角、底角的相关概念。

学生活动：

学生通过观察PPT图片，思考并回答问题。初步感知等腰三角形的特征。

意图与目标：(1)激发学生的学习兴趣

(2)复习旧知识，建立新旧知识的联系

资源与技术作用：PPT

作用：PPT展示，可以节省板书时间，提高学习效率，增强学生的注意力和学习兴趣。

教学环节二：探究新知

教师活动：

1.组织学生进行折纸活动：先让学生把一张长方形纸片对折，剪去阴影部分，再把它展开，观察△ABC有什么特点？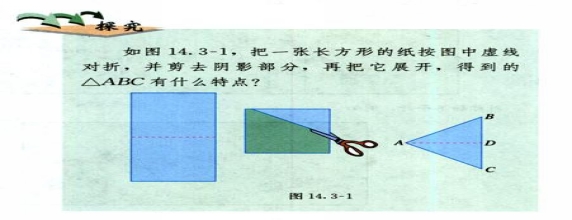

（1）提问：“通过观察折纸后的图形，你能得出什么结论？”

（2）以小组为单位讨论如何用全等三角形的知识证明性质1：“等边对等角”，讨论后师生交流，归纳证明方法。             

（3）最后老师用几何语言表述：“等边对等角”。

几何语言：在△ABC中

∵AB=AC(已知)

∴∠B=∠C(等边对等角)      

2.现在请同学们将等腰三角形的纸片对折，让两腰AB、AC重叠在一起，折痕为AD，如图，你能发现什么现象吗？请你尽可能多的写出结论。

（1）找一找：把剪出的等腰三角形ABC沿折痕对折，找出除“等边对等角”外重合的线段和角.

D

（2）猜一猜： 由这些重合的角，你能发现等腰三角形的另一性质吗？说一说你的猜想.

（3）师生交流：你猜想的依据是什么？

（4）教师板书几何语言：

如图,在△ABC中,

1.∵AB=AC, ∠1=∠2(已知)

∴BD=CD,AD⊥BC（等腰三角形三线合一）

2.∵AB=AC, BD=CD (已知)

∴∠1=∠2,AD⊥BC（等腰三角形三线合一）

3.∵AB=AC, AD⊥BC(已知)，

∴BD=CD, ∠1=∠2（等腰三角形三线合一）

强调:在这三种情况中，知道其中一种情况，就能推导出另两种情况。

（5）总结归纳:性质2:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一）。

（6）思考：画出任意一个等腰三角形的底角平分线，这个底角所对的腰上的中线和高，看看它们是否重合？

学生活动：

探究性质1时，以小组为单位讨论如何用全等三角形的知识证明性质1：“等边对等角”，讨论后师生交流，归纳证明方法。

探究性质2时，学生观察PPT,认真思考，回答老师所提问题             

资源与技术作用：

PPT展示，flsh动画演示，鸿合多屏互动，几何画板

作用：PPT展示，可以节省板书时间，提高学习效率，增强学生的注意力和学习兴趣；flsh动画演示，鸿合多屏互动，几何画板可以动态展示过程，辅助数学探究过程，突破教学难点。

意图与目标：

让学生经历一个定理的得到是:发现、猜想、证明这样的过程。

教学环节三:典例精析

教师活动：

教师引导学生，根据题意该如何分析，如何板书。

（1)等腰三角形的一个内角是50°，则这个三角形的底角的大小是(　　)

A．65°或50°             B．80°或40°

C．65°或80°             D．50°或80°

方法总结：等腰三角形的两个底角相等，已知一个内角，则这个角可能是底角也可能是顶角，要分两种情况讨论．

(2)如图，在△ABC中 ，AB=AC，点D在AC上，且BD=BC=AD，

求△ABC各角的度数.

归纳：在含多个等腰三角形的图形中求角时，常常利用方程思想，

通过内角、外角之间的关系进行转化求解.

学生活动：

1.观察PPT,认真思考，在练习本上独立完成。

          2.学生点评问题

资源与技术作用：

通过PPT演示，可以节省板书时间，提高学习效率，增强学生的注意力和学习兴趣，辅助学生的理解和记忆。

意图与目标：通过典型例题分析，让学生能初步运用等腰三角形的性质解决有关问题.

教学环节四:当堂训练

教师活动：学生讲过以后，教师点拨，总结方法。

1.以下是小明编制的习题.

已知△ABC是等腰三角形

①如果底角为40°，那么另外两个角的度数分别为（            )

②如果AB=AC，AC的垂直平分线与边AB相交所得的锐角是50°，那么∠B=

（     ）

(1) 请在①②处填入正确的答案;

(2)小杰根据小明的第②题，编制了一题:“如果AB=AC，AC的垂直平分线与边AB所在直线相交所得的锐角是50°，那么∠B=(             )

请在括号内填入正确的答案。

(3)  已知△ABC是等腰三角形，请尝试改编小明的第①题，使它的结果不唯一。（来自国家中小学智慧教育平台习题库，主要对应目标：811308）

2.古代测量水平线的仪器是由一个等腰三角形以及悬挂在顶点处的铅垂线组成.如图(1)所示，仪器中三角形的底边猜测是用绳子做成的，因为绳子的中点非常容易确定.测量时，调整底边的位置，如果铅垂线经过底边中点，就表明底边垂直于铅垂线，即底边是水平的，这就是古代的水准仪.

(1)请运用所学的等腰三角形的性质解释古代水准仪的原理;

(2)如图(2)是屋架的一种形式.在△ABC中，AB=AC，点B，C在横梁MN上.现有一把等腰直角三角形尺(底边的中点处有一颗钉子)、一个端点挂有铅锤的线绳(足够长)、一卷皮尺(足够长).如果要判断横梁MN是否水平，你会选择哪两个工具?如何使用?请用数学知识解释你的方法（忽略测量人员的人数）（来自国家中小学智慧教育平台习题库，主要对应目标：811308,811314） 学生活动：

1. 观察PPT,认真思考，咱练习本上独立完成习题；

2.小组讨论不会的知识；

3.找同学讲评习题。

资源与技术作用：

通过PPT演示，可以节省板书时间，提高学习效率，增强学生的注意力和学习兴趣，辅助学生的理解和记忆。

意图与目标：

通过当堂训练，让学生能运用等腰三角形的性质解决有关问题.

教学环节五:课堂小结

教师活动：教师引导学生总结本节课的学习内容

本节课你学到了什么？

学生活动：认真思考，回答老师的问题。

资源与技术作用：

通过PPT演示，让学生更直观知道本节课所学的知识有哪些。

意图与目标：

通过课堂小结，让学生形成知识体系。

教学环节六：课后作业

分层作业-因材施练

基础题

课本 P82习题 1、2、3

提高题

证明:等腰三角形两腰上的高相等

挑战题

探究:若等腰三角形的一个外角为110°，它的底角是多少度

教学环节七：板书设计

13.3.1等腰三角形

            定义:有两条边相等的三角形叫等腰三角形。

            性质1：等边对等角

            性质2：三线合一

教学环节八：教学反思

本节课《等腰三角形》，紧扣新课标要求，巧妙融合信息技术实现创新教学。课前通过智慧教育平台班级群，推送预习作业，精准定位知识薄弱点。在教学过程中，借助PPT,通过生活实例导入，激发学生学习兴趣。在探究新知中，通过折纸活动，学生充分猜想、验证，得出各种不同的结论，课中借助 PPT、flash动画、几何画板、多屏互动及时捕捉学生思路，依反馈动态调整讲解，助力学生突破重难点，达成高效学习，使课堂成为学生思维碰撞与知识建构的舞台。接着运用全等三角形的知识加以论证，使学生思维由形象直观过渡到抽象的逻辑演绎，层层展开，步步深入，使学生在生动有趣的数学活动中探究出等腰三角形的性质，从而实现教学目的。在典例精析中，通过例题，考察学生对基础知识的掌握情况，在当堂训练中，精选国家中小学智慧教育平台习题库中的习题，进行适当拔高，让学生通过上台板演、在练习本上独立做题、小组讨论、师生互讲等多元活动，深度参与知识建构。分层作业彰显因材施教理念，有效提升学生几何推理与应用能力。

在课堂上，充分运用现代信息技术的教学手段，在教学设计上，学生学习的兴趣增强了，对知识的探究也深入了，印象也比较深刻，明显比教师讲解有更强的作用，起到了良好的教学效果。